Research

My research interests broadly revolve arounds mathematical algorithms. In particular, I am interested in Machine Learning, Scientific Computing and Numerical algorithms with a focus on Numerical Linear Algebra.

You can find out about my work on my Google scholar page.

ML-based Weather prediction with Neural Operators

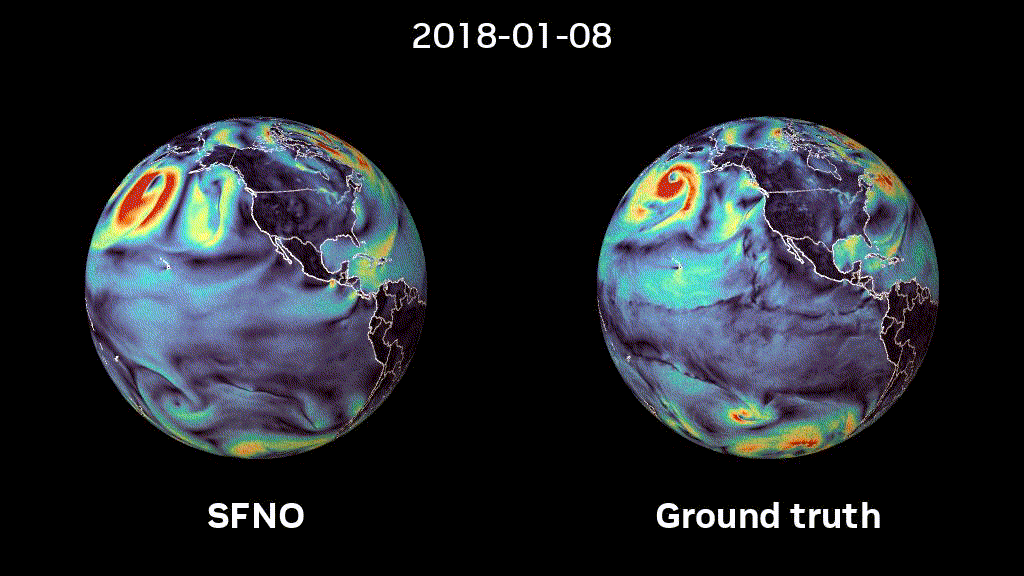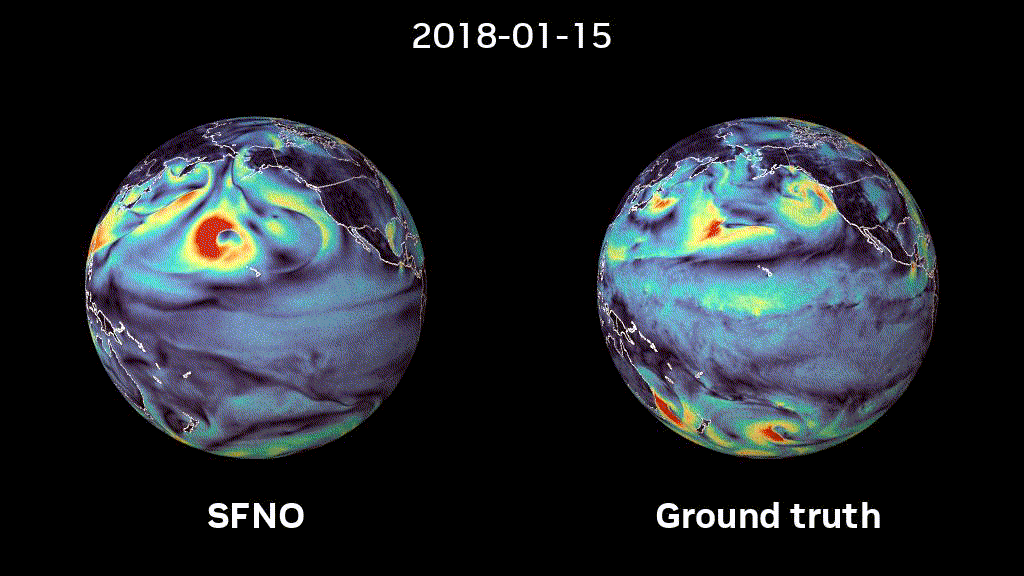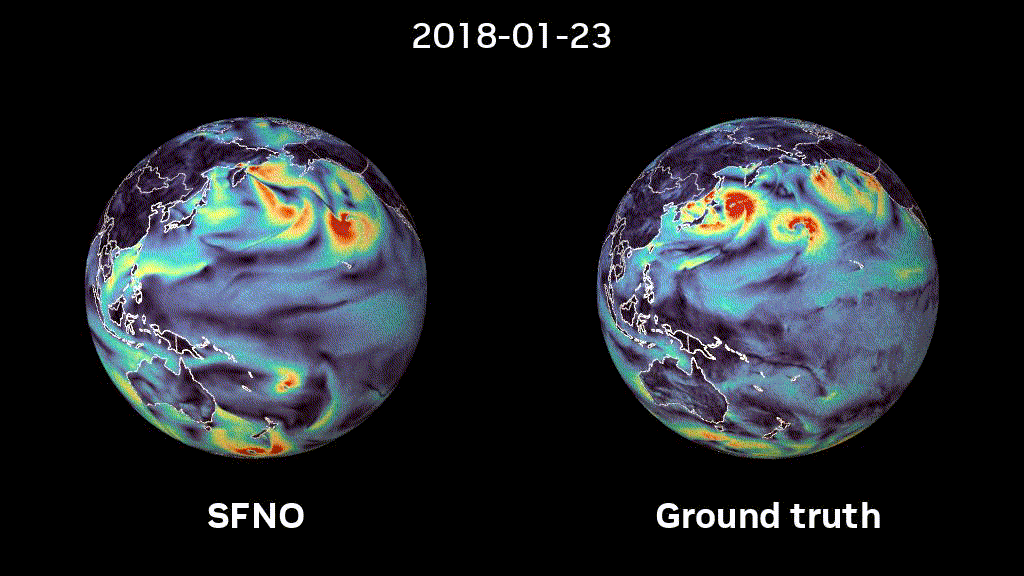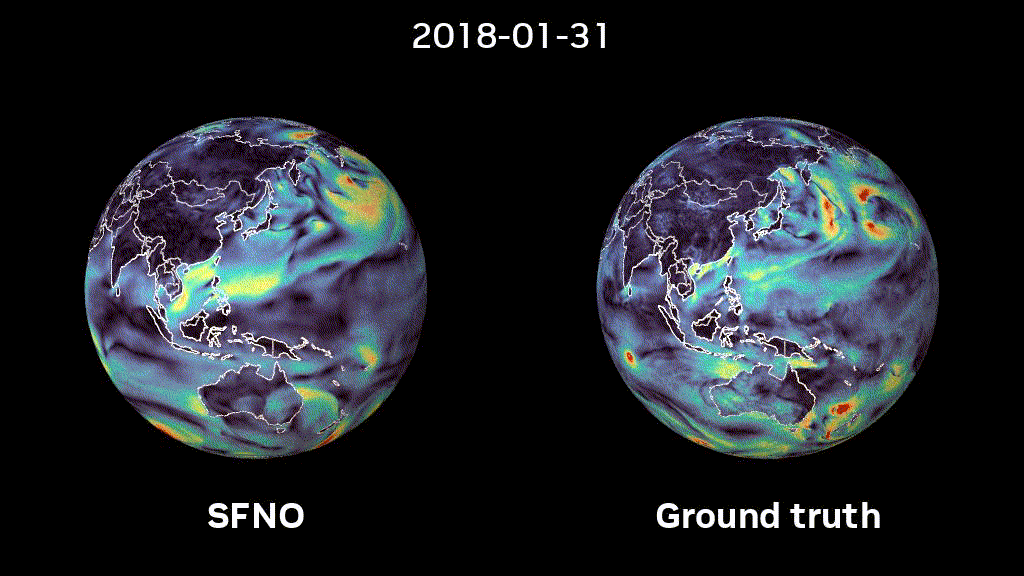
ML-based methods promise to greatly accelerate scientific computing. Recent advances in ML-based weather predicion have proven that these methods can compete with state-of-the-art classical weather prediction systems and even outperform them. However, how can we trust such models if they have been trained from data rather than from first-principles such as physical equations? One possible solution is to embue them with the same symmetries that we consider when formulating the physical equations that describe these. Our work on Spherical Fourier Neural Operators generalizes Fourier Neural Operators, a class of succesful models for modeling PDE systems, to spherical geometry. Find out more in our paper and a recently published NVIDIA blogpost.

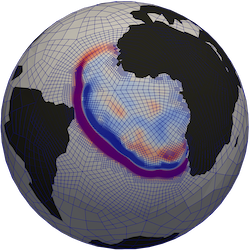
Sparse direct solvers for wave problems

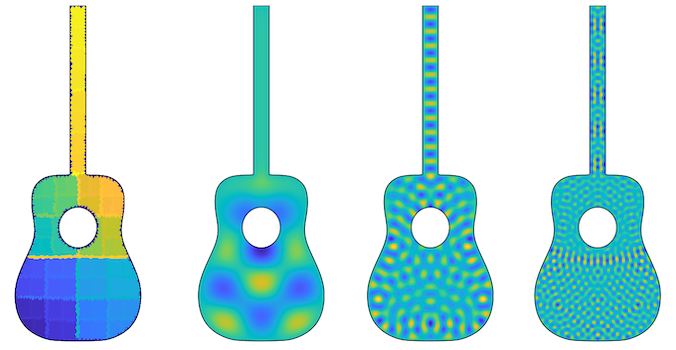
Sparse direct solvers aim to solve sparse linear systems of the form $A x = b$ efficiently, without relying on iterated matrix-vector multiplications such as Krylov subspace methods. This is particularly interesting for wave problems, where Krylov subspace methods typically require prohibitively many iterations to converge. Efficient sparse direct methods can be developed by exploiting physical properties of the underlying problem, which are encoded in the matrix $A$. More precisely, we use so-called hierarchical matrices to compress the dense fill-in that arises when $A$ is factored. This class of solvers can be used to solve problems such as the Helmholtz problem, which is illustrated below. These problems are typically difficult because of their indefinite nature and the spectrum of $A$. Not only can these methods solve the problem exactly, they can also serve as approximate solvers, which in turn can be used as preconditioners for iterative methods. You can read more about our work on this topic in our paper or in my PhD dissertation.

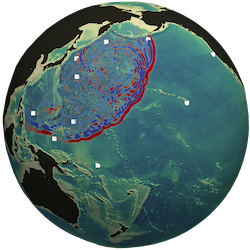
Discontinuous Galerkin methods for tsunami simulations

Discontinuous Galerkin methods are a promising class of methods for solving PDEs numerically. This is especially true for hyperbolic PDEs, where these methods achieve a high accuracy per degree of freedom. Moreover, they offer high locality and flexibility, which makes them especially suitable for high performance computing and large-scale problems such as weather prediction and Tsunami simulations. We demonstrate this by adapting the discontinuous Galerkin method to the simulation of global-scale Tsunami events. More precisely, we use the spherical formulation of the shallow water equations and adapt the discontinuous Galerkin formalism to these equations, dealing with important properties such as well-balancedness, wetting and drying, as well as mesh adaptivity. You can check out the videos below and find more details in our papers here and here.