Page Not Found
Page not found. Your pixels are in another canvas.
A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Page not found. Your pixels are in another canvas.
About me
CV
This is a page not in th emain menu
Research
Software
Published:
Gaussian Processes (GPs) generalize Gaussian distributions to random variables that are functions (stochastic processes). As such, they are a powerful tool for regression and Bayesian inference. In the past years, they have received increased attention due to the interest in machine learning. An intriguing connection between GPs and neural network exists when the width of layers in feed-forward neural networks tends towards infinity. For a specific choice of the prior distributions that governs the network parameters, the resulting network will be a GP.
Published:
This is the first post in a series of posts that I am planning to write on the topic of machine learning. This article introduces fundamental algorithms in numerical optimization. For now, this is the Gradient Descent and Netwon algorithm. I might extend it with momentum based methods and conjugate gradient methods in the future. All of the posts are essentially Jupyter notebooks that I will publish in this repository.
Short description of portfolio item number 1
Short description of portfolio item number 2 
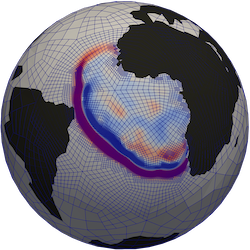
Boris Bonev, Jan S. Hesthaven, Francis X. Giraldo, Michal A. Kopera
Published in Journal of Computational Physics (JCP), 2018
Prantl, Lukas; Bonev, Boris; Thuerey Nils
Published in International Conference on Learning Representations (ICLR), 2018
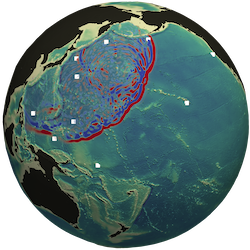
Hajihassanpour, Mahya; Bonev, Boris; Hesthaven, Jan S.
Published in Ocean Modelling, 2019
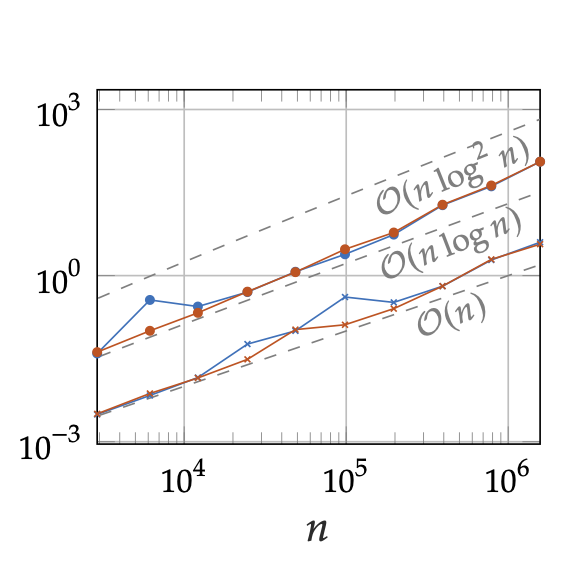
Boris Bonev, Jan S. Hesthaven
Published in SIAM: Journal on Scientific Computing, 2020
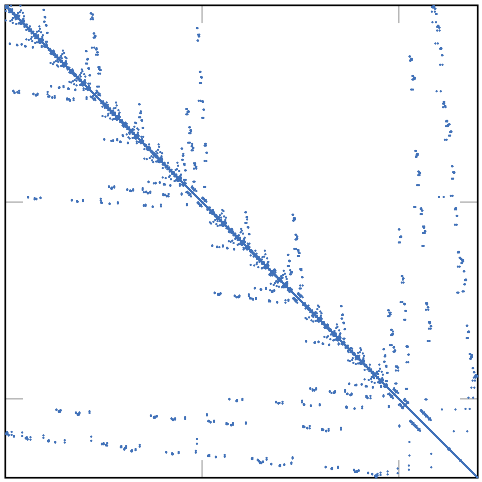
Boris Bonev
Published in PhD Thesis, Applied Mathematics, EPFL, 2021
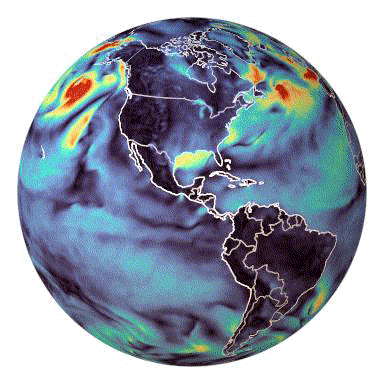
Boris Bonev, Thorsten Kurth, Christian Hundt, Jaideep Pathak, Maximilian Baust, Karthik Kashinath, Anima Anandkumar
Published in International Conference on Machine Learning (ICML), 2023
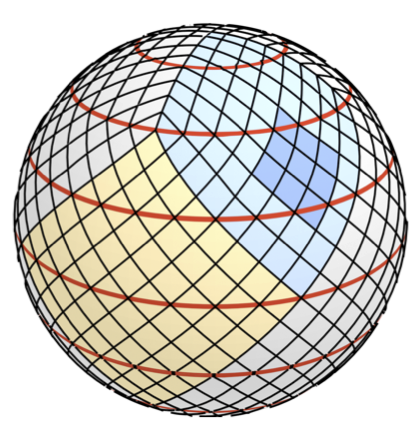
Matthias Karlbauer, Nathaniel Cresswell-Clay, Dale R Durran, Raul A Moreno, Thorsten Kurth, Boris Bonev, Noah Brenowitz, Martin V Butz
Published in under review, 2023
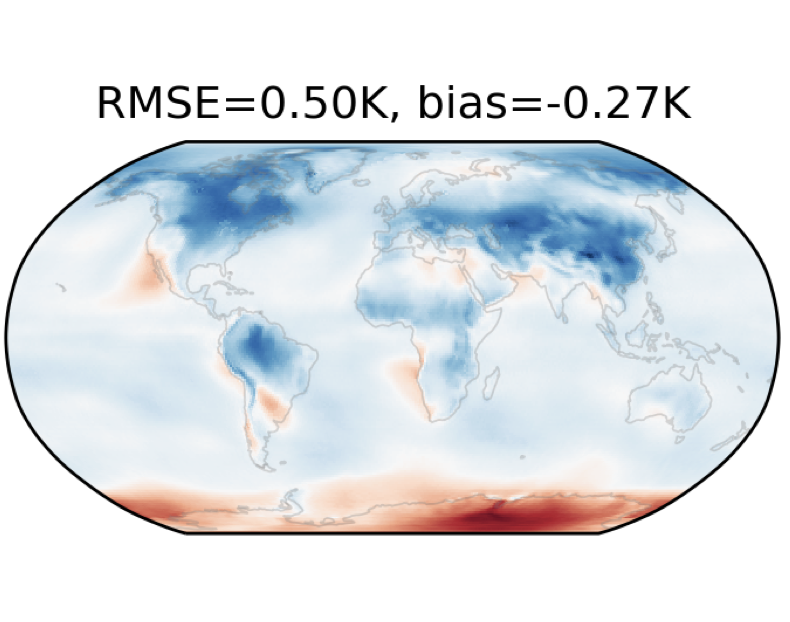
Oliver Watt-Meyer, Gideon Dresdner, Jeremy McGibbon, Spencer K. Clark, Brian Henn, James Duncan, Noah D. Brenowitz, Karthik Kashinath, Michael S. Pritchard, Boris Bonev, Matthew E. Peters, Christopher S. Bretherton
Published in Under review, 2023
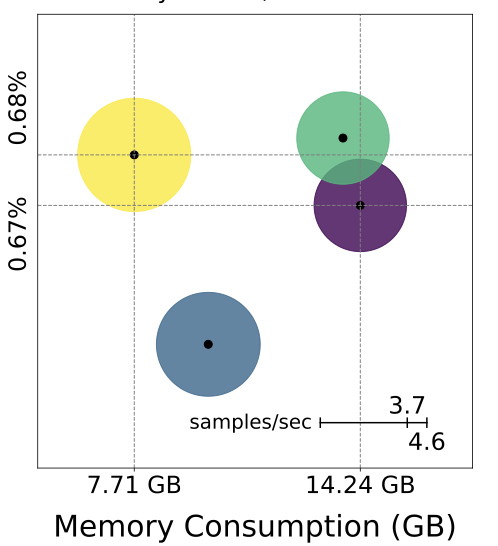
Renbo Tu, Colin White, Jean Kossaifi, Boris Bonev, Gennady Pekhimenko, Kamyar Azizzadenesheli, Anima Anandkumar
Published in International Conferenceon Learning Representations (ICLR), 2023
Noah D. Brenowitz, Yair Cohen, Jaideep Pathak, Ankur Mahesh, Boris Bonev, Thorsten Kurth, Dale R. Durran, Peter Harrington, Michael S. Pritchard
Published in under review, 2024
Miguel Liu-Schiaffini, Julius Berner, Boris Bonev, Thorsten Kurth, Kamyar Azizzadenesheli, Anima Anandkumar
Published in under review, 2024
Published:
Discontinuous Galerkin methods have desirable properties, which make them suitable for the com- putation of wave problems. Being parallelizable and hp-adaptive makes them attractive for the simulation of large-scale tsunami propagation. In order to retrieve such a scheme, we formulate the shallow water equations on the spherical shell and apply the discontinuous Galerkin discretiza- tion to construct a numerical method which is able to handle the effects of curvature and Coriolis forces naturally. Common challenges in solving the shallow water equations numerically are well- balancedness and wetting/drying. To overcome this, we utilize a method based on a timestep restriction, which guarantees the positivity of the numerical solution. Moreover, we show that our discretization yields a well-balanced numerical scheme. In this talk we will present our method as well as the numerical results, that we have obtained with our implementation.
Published:
We present a novel method for the simulation of large scale tsunami events using a high-order discontinuous Galerkin discretization of the spherical shallow water equations. This requires a well-balanced discretization, which cannot rely on exact quadrature, due to the curved mesh. We achieve this by splitting the well-balanced condition into individual problems for the flux and volume terms. As it turns out, this approach has significant advantages: It allows the construction of non-conforming, well-balanced flux discretizations. Thus we can perform non-conforming mesh refinement, all while preserving the well-balanced property of the scheme. More importantly, we are able to develop a new method for handling wet/dry transitions. In contrast to other wetting/drying methods, this method is well-balanced and able to handle wetting/drying at any order - all without the introduction of further model assumptions such as artificial viscosity, porosity or cancellation of gravity. We demonstrate our new method for both the one-dimensional and spherical shallow water equa- tions. In the latter case, we perform a simulation of the 2011 Tohoku tsunami and validate our results with real-world buoy data.
Published:
While physics aims to describe nature in terms of mathematics, numerical mathematics aims to represent nature on a computer. This talk will show how we develop a computational model with the example of large-scale tsunami simulations. Finally, we will see how we can use these models to gain a better understanding of our world. Numerical mathematics brings together physics, computer science, engineering and of course, mathematics.
Workshop, University 1, Department, 2015
This is a description of a teaching experience. You can use markdown like any other post.
Undergraduate course, EPFL, Math department, 2019
Principal assistant for the course “Probabilité et Statistique”, teaching engineering students the fundamentals of probability theory and statistics.